DEFINISI PROPOSISI
Sebuah proposisi atau statement sebuah kalimat
deklaratif yang memiliki tepat satu
nilai kalimat kebenaran yaitu “BENAR”
(B) atau “SALAH” (S).
TABEL KEBENARAN
Pada pembicaraan ini dan seterusnya kita
hanya membicarakan pernyataan-pernyataan
saja. Pernyataan-pernyataan sederhana
digandengkan menjadi pernyataan majemuk
(tersusun) dengan menggunakan kata-kata
perangkai (penghubung). Kata-kata perangkai itu
adalah :
(1) “atau” dengan simbol “ Ú ”
(2) “dan” dengan simbol “&” atau “ Ù
”
(3) “apabila …. maka….” dengan simbol “
Þ ”
(4) “bila dan hanya bila” dengan simbol
“ Û ”
Sedangkan negasi (sangkalan) suatu
pernyataan digunakan kata-kata “tidak benar
bahwa” yang diberi simbol “-” di depan
pernyataan yang disangkal (diingkar). Di depan
telah dikatakan bahwa
pernyataan-pernyataan diberi simbol dengan huruf alfabet kecil: a, b,
c, d, ….. Sedangkan nilai “Benar” atau “Salah” suatu pernyataan
disingkat berturut-turut
dengan “B” atau “S”.
A. Negasi (Sangkalan/Ingkaran) ”
- “
Negasi suatu pernyataan ialah suatu
pernyataan yang bernilai salah apabila pernyataan
semula bernilai benar, dan bernilai
benar apabila pernyataan semula bernilai salah.
Definisi ini dapat dinyatakan dalam
suatu tabel yang disebut tabel kebenaran untuk
negasi suatu pernyataan sebagai berikut:
Tabel 3.1.Tabel Nilai Kebenaran
Contoh : Jika a:
“Ida suka mangga”
maka –a : “Tidak benar bahwa Ida suka mangga”.
B. Konjungsi Dua Pernyataan ”a^b”
Konjungsi dua pernyataan a dan b ditulis
“a & b” (dibaca “a dan b”) bernilai B
(benar), hanya apabila kedua pernyataan
tunggalnya bernilai B, dan untuk nilai-nilai
kebenarana dan b lainnya,
maka “a & b” bernilai S (salah).
Definisi tersebut dapat dinyatakan dalam
suatu tabel kebenaran (tabel 3.2) konjungsi
dua pernyataan a dan b.
Tabel 3.2.Tabel Nilai Kebenaran
Konjungsi Dua Pernyataan a dan b
Contoh :
1) Misalkan “a” menyatakan
“Tembok itu berwarna hitam”, maka negasi a yaitu “-a”
menyatakan “Tidak benar bahwa tembok itu
berwarna hitam”. Lebih ringkas dikatakan
“Tembok itu tidak berwarna hitam”.
Apabila “b” menyatakan “Tembok
itu berwarna putih”, maka b bukan negasi dari a.
Sebab apabila kenyataannya tembok itu
berwarna hijau, maka baik a maupun b kedua
pernyataan bernilai salah. Hal ini
bertentangan dengan definisi 3.1.
2) Jika p dan q keduanya bilangan real,
maka negasi dari “p > q” adalah “tidak benar bahwa
p> q”. Tidak benar bahwa p > q
tidak berarti bahwa p < q, sebab jika kenyataannya p =
q, maka baik p > q maupun p < q
keduanya bernilai salah. Sehingga negasi dari “p > q”
adalah “p £ q”.
a -a -(-a)
Catatan: Pernyataan dan negasinya mempunyai nilai-nilai kebenaran
yang selalu berlainan,
artinya jika suatu pernyataan diketahui
bernilai B, maka negasinya bernilai S dan
sebaliknya jika suatu pernyataan
diketahui bernilai S, maka negasinya bernilai B.
C. Disjungsi Dua Pernyataan
Disjungsi dua pernyataan a dan b ditulis
“a Ú b” (dibaca: “a atau b”) bernilai S hanya
apabila dua pernyataan tunggalnya
bernilai S, sedangkan untuk nilai-nilai kebenaran a
danb lainnya, maka “a Ú b” bernilai B.
Definisi ini dapat dinyatakan dalam
suatu tabel kebenaran disjungsi dua pernyataan a
danb (tabel 3.3) sebagai berikut:
Tabel 3.3.Tabel Nilai Kebenaran
Disjungsi Dua Pernyataan a dan b
Contoh:
1) “7 adalah bilangan prima atau 7 lebih
besar dari 8” adalah disjungsi yang bernilai benar
(sesuai baris kedua dari tabel 3.3).
2) “5 adalah bilangan prima atau 5
membagi habis 20” adalah suatu dijungsi yang bernilai
benar.
3) “ 6 adalah faktor dari 9 atau 4 + 7 =
10” adalah suatu dijungsi yang bernilai salah.
4) Apabila x bilangan nyata, maka (x –
1)(x – 5) = 0 dipenuhi jika x = 1 Ú x = 5.
Disjungsi dua pernyataan yang
didefinisikan sesuai dengan tabel 3.3 disebut disjungsiinklusif.
Disjungsi jenis lain disebut disjungsi
eksklusif. Disjungsi eksklusif dua pernyataan
adan b disimbolkan sebagai “a Ú b” (dibaca “atau a atau b”) dan didefinisikan sesuai
dengan
tabel 3.4. Dalam buku ini, apabila
ditentukan suatu disjungsi tanpa keterangan apa-apa, maka
yang dimaksud adalah disjungsi inklusif.
Tabel 3.4.Tabel Nilai Kebenaran
Disjungsi Eksklusif dari a dan b.
D. Implikasi (Kondisional) Dua Pernyataan
Implikasi dua pernyataan a dan b diberi
simbol “a Þ b” (dibaca “apabila a maka b”).
adisebut pendahulu
(antecedent) dan b disebut pengikut (consequent).
Implikasi “a Þ b” bernilai S hanya apabila
pendahulu a bernilai B dan pengikut b
bernilai S, untuk nilai-nilai kebenaran a dan b lainnya,
maka implikasi “a Þ b”
bernilai B.
Definisi tersebut dapat dinyatakan dalam
suatu tabel kebenaran implikasi
aÞ b (tabel 3.5) berikut.
Tabel 3.5.Tabel Nilai Kebenaran
Implikasi a Þ b
Dalam percakapan sehari-hari pernyataan majemuk “apabila … maka
…” biasanya
ada suatu hubungan antara pendahulu dan
pengikut.
Contoh:
Apabila matahari terbit dari barat, maka
Siti lulus ujian.
Kalimat ini sering kita dengar, dan
dimaksudkan bahwa mustahil Siti akan lulus dalam
menempuh ujiannya. Meskipun dalam
implikasi itu tidak ada hubungan antara pendahulu
(matahari terbit dari barat) dan
pengikut (Siti lulus ujian). Implikasi itu bernilai benar, sebab
pendahulunya bernilai salah.
Perhatikan tabel nilai kebenaran
implikasi (tabel 3.5), maka kita dapat
menyimpulkan :
(1) Implikasi
selalu bernilai benar, apabila pendahulunya bernilai salah, tanpa
memperhatikan nilai kebenaran
pengikutnya (sesuai baris ke 3 dan 4 dalam tabel
3.5).
Nilai kebenaran pengikutnya, baik Benar
atau Salah, jika pendahulunya bernilai Salah,
maka implikasi tersebut bernilai Benar.
(2) Implikasi
selalu bernilai benar, apabila pengikutnya bernilai benar, tanpa
memperhatikan nilai kebenaran dari
pendahulunya (sesuai baris ke 1 dan 3). Tanpa
mengetahui nilai kebenaran pendahulu,
jika diketahui pengikutnya bernilai Benar, maka
implikasi tersebut bernilai Benar.
Implikasi yang dipelajari dalam
Matematika adalah implikasi yang didefinisikan
seperti dalam tabel 3.5. Implikasi
semacam ini disebut implikasi
material.Sedang implikasi
yang dijumpai dalam percakapan
sehari-hari disebut implikasi
biasa (ordinary implication).
Apabila diketahui bahwa “a Þ b” bernilai benar, maka:
(1) adisebut syarat cukup bagi b, atau
(2) bdisebut syarat perlu bagi a.
Perhatikan bahwa suatu syarat perlu
belum tentu merupakan syarat cukup.
Definisi implikasi lanjut :
Apabila diketahui “a Þb” maka
(1) bÞ a disebut konvers dari a Þb
(2) – a Þ – b disebut invers dari a Þb
(3) – b Þ – a disebut kontraposisi (kontrapositif) dari a Þb .
Definisi 3.5 ini dapat dinyatakan dengan
skema sebagai berikut:
Tabel 3.6 adalah tabel nilai kebenaran suatu implikasi beserta
konvers, invers, dan
kontraposisinya.
Memperhatikan tabel 3.6 ini, kita dapat
menarik beberapa kesimpulan, yaitu:
(1) Implikasi mula-mula ( aÞ b )
dan konversnya tidak selalu mempunyai nilai
kebenaran yang sama.
(2) Implikasi mula-mula dan inversnya
tidak selalu mempunyai nilai kebenaran yang
sama.
(3) Implikasi mula-mula selalu mempunyai
nilai kebenaran yang sama dengan
kontraposisinya, dikatakan bahwa “ a Þ b ekuivalen
dengan – b Þ – a ”
dan
ditulisa Þ b ek
– b Þ – a .
Tabel 3.6.Tabel Nilai Kebenaran Implikasi a Þ b
beserta Konvers, Invers dan
Kontraposisnya
E. Biimplikasi (Bikondisional)
Biimplikasi a dan b (disimbolkan
dengan “a Ûb” )
bernilai benar apabila kedua
pernyataan tunggalnya mempunyai nilai
kebenaran yang sama, dan mempunyai
bernilai salah apabila kedua pernyataan
tunggalnya mempunyai nilai kebenaran yang
berbeda.
Tabel 3.7.Tabel Nilai Kebenaran
Biimplikasi dari a dan b.
Teorema: a Û b
ek ( a Þ b )
& ( b Þ a )
Bukti: Untuk membuktikan kebenaran teorema itu
diperlihatkan tabel nilai kebenarannya sebagai berikut:
Terlihat bahwa urutan nilai kebenaran pada kolom 3 sama dengan
urutan nilai
kebenaran pada kolom 6, berarti:
aÛ b
ek ( a Þ b )
& (b Þ a )
Pada implikasi a Þ b ,a adalah syarat cukup bagi b, dan pada implikasi b Þ a , a
adalah syarat perlu bagi b. Sehingga a Û b berarti a adalah
syarat cukup dan perlu bagi b
dan sebaliknya..
Contoh:
Apabila ketiga sisi suatu segitiga sama
panjang maka segitiga itu samasisi.
Dimaksudkan bahwa “ketiga sisi suatu
segitiga sama panjang bila dan hanya bila segitiga itu
sama sisi”.
Selanjutnya kata perangkai “bila dan
hanya bila” disingkat “bhb”. Kita telah
menggunakan singkatan “ek” untuk
“ekuivalen”. Dua pernyataan dikatakan ekuivalen
apabila nilai-nilai kebenarannya sama.
Bandingkanlah
aÛ b dengana ek b. Kedua pernyataan ini
mempunyai nilai kebenaran sama.
F. Negasi-Negasi dari Konjungsi,
Disjungsi, Implikasi dan Biimplikasi.
Untuk menentukan negasi-negasi
konjungsi, disjungsi, implikasi, dan biimplikasi
disusun tabel-tabel kebenarannya dalam
satu tabel (tabel 3.9)
Tabel 3.9
Misalkan kita akan menentukan negasi
dari (a & b), yaitu –(a & b),
nilai-nilai kebenarannya terlihat pada kolom ke-8. Nilai-nilai kebenaran pada
kolom itu terdiri atas satu S dan diikuti berturut-turut tiga B. Hal ini hanya
terjadi pada pernyataan majemuk dengan kata penghubung “ Ú ”, yaitu –a Ú -b.
Jadi –(a
& b) ek –aÚ –b
Nilai-nilai kebenaran dari –(a Ú b) berturut terdiri atas tiga S dan
satu B (lihat kolom 9). Hal ini hanya terjadi pada pernyataan majemuk dengan
kata penghubung “&”, yaitu -a
& -b.
Jadi –(a Ú b) ek -a & -b.
Nilai-nilai kebenaran dari –(a Þ b) terdiri atas tiga S dan satu B
(lihat kolom 10). Hal ini hanya terjadi pada nilai-nilai kebenaran pernyataan
majemuk dengan kata penghubung “&”, yaitu a
& -b. Jadi
–(a Þ b) ek a & -b.
Kita telah mengetahui bahwa b a Û
ek ( a Þ b )
& ( b Þ a )
Maka–( a Û b )
ek –(( a Þ b )
& ( b Þ a ))
ek –( a Þ b )
Ú –( b Þ a )
ek (a
& -b) Ú (b & -a)
Jadi –( a Û b ) ek (a & -b) Ú (b & -a)
 merupakan kalimat terbuka karena mengandung variabel
merupakan kalimat terbuka karena mengandung variabel 

 .
. .
. atau
atau  , yang dibaca dengan “jika”. Misal
, yang dibaca dengan “jika”. Misal  maka dibaca “jika P maka Q. Pada tabel kebenaran, hasilnya benar jika kedua pernyataannya benar atau kedua pernyataannya salah.
maka dibaca “jika P maka Q. Pada tabel kebenaran, hasilnya benar jika kedua pernyataannya benar atau kedua pernyataannya salah. atau
atau  . Misal
. Misal  , maka dibaca “P jika dan hanya jika Q”.
, maka dibaca “P jika dan hanya jika Q”.
 , maka berlaku:
, maka berlaku:



 .
.


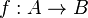




 dengan a1 tidak sama dengan a2 berlakuf(a1) tidak sama dengan f(a2). Dengan kata lain, bila a1 = a2 maka f(a1) sama dengan f(a2).
dengan a1 tidak sama dengan a2 berlakuf(a1) tidak sama dengan f(a2). Dengan kata lain, bila a1 = a2 maka f(a1) sama dengan f(a2).
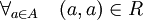




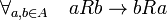
 genap” adalah relasi simetrik, karena untuk sembarang x dan y yang kita pilih, jika memenuhi relasi tersebut, maka dengan menukarkan nilai y dan x, relasi tersebut tetap dipenuhi. Misalnya untuk pasangan (5, 3) relasi tersebut dipenuhi, dan untuk (3, 5) juga.
genap” adalah relasi simetrik, karena untuk sembarang x dan y yang kita pilih, jika memenuhi relasi tersebut, maka dengan menukarkan nilai y dan x, relasi tersebut tetap dipenuhi. Misalnya untuk pasangan (5, 3) relasi tersebut dipenuhi, dan untuk (3, 5) juga.



 bersifat anti-simetrik, karena
bersifat anti-simetrik, karena  mengakibatkan
mengakibatkan  . Demikian juga jika ada p dan q yang terhadap mereka berlaku
. Demikian juga jika ada p dan q yang terhadap mereka berlaku  dan
dan 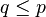 berarti
berarti 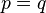 .
.
